879
California State Professional Engineer Registration Examination
The following problem is taken from Easypower Demo 7.0 Protection-1.dez sample file. The problem will be solved using the MVA method implemented in the online short circuit calculator presented on this web-site. Fault current values at nodes a) to j) need to be calculated. The resulting short circuit current values will be compared with the respective values produced by ESA Easypower 7.0.
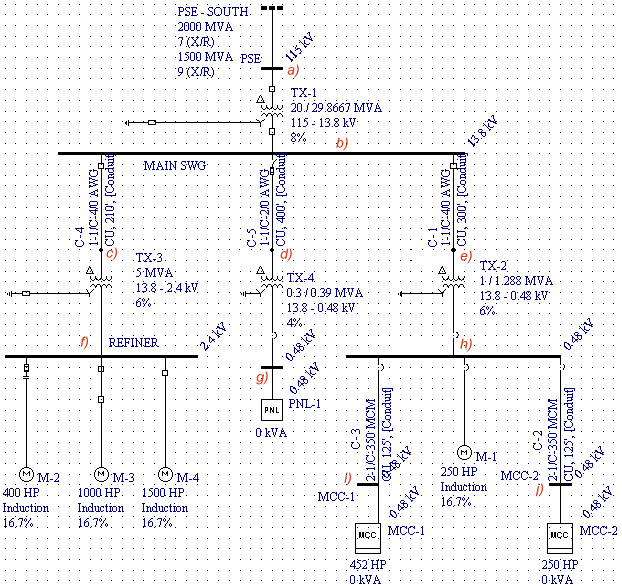
MVA sequence diagram below shows positive and zero sequence networks for the above power system. Since the positive and negative sequence impedances are the same in a static symmetrical system, conversion of a positive sequence network to a negative sequence network is accomplished by changing if necessary only the impedances that represent rotating machinery and by omitting emfs. Three phase synchronous generators and motors have internal voltages of positive sequence only, since they are designed to generate balanced voltages. Electromotive forces are omitted on the assumption of balanced generated voltages and the absence of negative sequence voltages induces from outside sources. In our example, negative sequence network is identical to positive sequence with emf sources removed.

Full scale short circuit study requires analysis of positive, negative and zero sequence networks. The table below shows entry data required for the analysis. RES MVA and RES X/R columns show the resulting MVA and X/R quantities for the respective sequences.
| POSITIVE SEQUENCE NETWORK | ||||||||
| ID | LABEL | SC MVA | X/R | DESCRIPTION | P A R E N T | RES MVA | RES X/R | N O D E |
| 1 | PSE | 2000 | 7 | PSE-SOUTH 2000MVA S.E. | 0 | 2017 | 7.03 | a |
| 2 | TX-1 | 250 | 22.3 | TX-1 20 MVA Z=8% D-YRG | 1 | 240.67 | 17.4 | b |
| 3 | C-4 | 11050 | 0.9 | 1-1/C-4/0 AWG 210 FEET CU | 2 | 237.1 | 14.4 | c |
| 4 | C-5 | 4205 | 0.6 | 1-1/C-2/0 AWG 400 FEET CU | 2 | 229 | 11.9 | d |
| 5 | C-1 | 7735 | 0.9 | 1-1/C-4/0 AWG 300 FEET CU | 2 | 235.1 | 13.1 | e |
| 6 | TX-3 | 83.3 | 12.6 | TX-3 5 MVA Z=6% D-YRG | 3 | 77.9 | 14.54 | f |
| 7 | TX-4 | 7.5 | 3.7 | TX-4 0.3 MVA Z=4% D-YG | 4 | 7.27 | 3.8 | g |
| 8 | TX-2 | 16.67 | 5.7 | TX-2 1 MVA Z=6% D-YG | 5 | 21.04 | 5.7 | h |
| 9 | M-2 | 2.38 | 17.6 | 398KVA 16.7%Z 17.62X/R | 6 | |||
| 10 | M-3 | 5.96 | 25 | 996KVA 16.7%Z 24.97X/R | 6 | |||
| 11 | M-4 | 8.94 | 28.4 | 1494KVA 16.7%Z 28.43X/R | 6 | |||
| 12 | PNL-1 | 0 | 0 | 0 SCMVA 480V PANEL | 7 | |||
| 13 | C-3 | 66.8 | 1 | 2-1/C-350 MCM 125 FEET CU | 8 | 17.6 | 3.43 | I |
| 14 | C-2 | 66.8 | 1 | 2-1/C-350 MCM 125 FEET CU | 8 | 17.1 | 3.26 | j |
| 15 | MCC-1 | 2.67 | 4.5 | 446KVA 16.7%Z 4.5X/R | 13 | |||
| 16 | M-1 | 1.47 | 14.2 | 247KVA 16.7%Z 14.21X/R | 8 | |||
| 17 | MCC-2 | 1.48 | 4.5 | 247KVA 16.7%Z 4.5X/R | 14 | |||
| NEGATIVE SEQUENCE NETWORK | ||||||||
| ID | LABEL | SC MVA | X/R | DESCRIPTION | P A R E N T | RES MVA | RES X/R | N O D E |
| 1 | PSE | 2000 | 7 | PSE-SOUTH 2000MVA S.E. | 0 | 2017 | 7.03 | a |
| 2 | TX-1 | 250 | 22.3 | TX-1 20 MVA Z=8% D-YRG | 1 | 240.67 | 17.4 | b |
| 3 | C-4 | 11050 | 0.9 | 1-1/C-4/0 AWG 210 FEET CU | 2 | 237.1 | 14.4 | c |
| 4 | C-5 | 4205 | 0.6 | 1-1/C-2/0 AWG 400 FEET CU | 2 | 229 | 11.9 | d |
| 5 | C-1 | 7735 | 0.9 | 1-1/C-4/0 AWG 300 FEET CU | 2 | 235.1 | 13.1 | e |
| 6 | TX-3 | 83.3 | 12.6 | TX-3 5 MVA Z=6% D-YRG | 3 | 77.9 | 14.54 | f |
| 7 | TX-4 | 7.5 | 3.7 | TX-4 0.3 MVA Z=4% D-YG | 4 | 7.27 | 3.8 | g |
| 8 | TX-2 | 16.67 | 5.7 | TX-2 1 MVA Z=6% D-YG | 5 | 21.04 | 5.7 | h |
| 9 | M-2 | 2.38 | 17.6 | 398KVA 16.7%Z 17.62X/R | 6 | |||
| 10 | M-3 | 5.96 | 25 | 996KVA 16.7%Z 24.97X/R | 6 | |||
| 11 | M-4 | 8.94 | 28.4 | 1494KVA 16.7%Z 28.43X/R | 6 | |||
| 12 | PNL-1 | 0 | 0 | 0 SCMVA 480V PANEL | 7 | |||
| 13 | C-3 | 66.8 | 1 | 2-1/C-350 MCM 125 FEET CU | 8 | 17.6 | 3.43 | I |
| 14 | C-2 | 66.8 | 1 | 2-1/C-350 MCM 125 FEET CU | 8 | 17.1 | 3.26 | j |
| 15 | MCC-1 | 2.67 | 4.5 | 446KVA 16.7%Z 4.5X/R | 13 | |||
| 16 | M-1 | 1.47 | 14.2 | 247KVA 16.7%Z 14.21X/R | 8 | |||
| 17 | MCC-2 | 1.48 | 4.5 | 247KVA 16.7%Z 4.5X/R | 14 | |||
| ZERO SEQUENCE NETWORK | ||||||||
| ID | LABEL | SC MVA | X/R | DESCRIPTION | P A R E N T | RES MVA | RES X/R | N O D E |
| 1 | PSE | 1500 | 9 | PSE-SOUTH 1500 ZS MVA S.E. | 0 | 1500 | 9 | a |
| 2 | TX-1 D | 0 | 22.3 | TX-1 20 MVA DELTA SIDE | 1 | |||
| 1 | TX-1 RY | 3.17 | 0 | 19.9 OHM GROUND RESISTANCE | 0 | |||
| 2 | TX-1 Y | 294 | 22.25 | TX-1 20 MVA Z0=6.8% WYE SIDE | 1 | 3.18 | 0.06 | b |
| 3 | C-4 | 1210 | 1 | 1-1/C-4/0 AWG 210 FEET CU | 2 | 3.17 | 0.07 | c |
| 4 | C-5 | 463 | 1.6 | 1-1/C-2/0 AWG 400 FEET CU | 2 | 3.15 | 0.09 | d |
| 5 | C-1 | 846 | 1 | 1-1/C-4/0 AWG 300 FEET CU | 2 | 3.17 | 0.08 | e |
| 6 | TX-3 D | 0 | 0 | TX-3 5 MVA DELTA SIDE | 3 | |||
| 7 | TX-4 D | 0 | 0 | TX-4 0.3 MVA DELTA SIDE | 4 | |||
| 8 | TX-2 D | 0 | 0 | TX-2 1 MVA DELTA SIDE | 5 | |||
| 1 | TX-3 RY | 0.27 | 0 | 6.9 OHM GROUND @ 2.4KV | 0 | |||
| 2 | TX-3 Y | 98 | 12.58 | TX-3 5 MVA Z0=5.1% WYE SIDE | 1 | 0.27 | 0 | f |
| 3 | M-2 | 0 | 0 | 398KVA 16.7%Z IND MOTOR | 2 | |||
| 4 | M-3 | 0 | 0 | 996KVA 16.7%Z IND MOTOR | 2 | |||
| 5 | M-4 | 0 | 0 | 1494KVA 16.7%Z IND MOTOR | 2 | |||
| 1 | TX-4 Y | 8.82 | 3.68 | TX-4 .3 MVA Z0=3.4% WYE SIDE | 0 | 8.82 | 3.68 | g |
| 2 | PNL-1 | 0 | 0 | 0 SCMVA 480V PANEL | 1 | |||
| 1 | TX-2 Y | 19.6 | 5.68 | TX-2 1 MVA Z0=5.1% WYE SIDE | 0 | 19.6 | 5.7 | h |
| 2 | C-3 | 7.4 | 1 | 2-1/C-350 MCM 125 FEET CU | 1 | 5.58 | 1.4 | I |
| 3 | C-2 | 7.4 | 1 | 2-1/C-350 MCM 125 FEET CU | 1 | 5.58 | 1.4 | j |
| 4 | MCC-1 | 0 | 0 | 446KVA 16.7%Z 4.5X/R | 2 | |||
| 5 | M-1 | 0 | 0 | 247KVA 16.7%Z 14.21X/R | 1 | |||
| 6 | MCC-2 | 0 | 0 | 247KVA 16.7%Z 4.5X/R | 3 |
Table below is a compilation of the kA produced by the online short circuit calculator, system line to line voltages and Easypower 7.0 calculation results at potential fault points. The resulting short circuit current values in kA are obtained by running MVA to KA converter.
| N O D E | LABEL | VLL, kV | MVA 1 | MVA 2 | MVA 0 | X/R 1 | X/R 2 | X/R 0 | 3 phase, kA | EP 3 phase, kA | L-G, kA | EP L-G, kA | L-L, kA | EP L-L, kA |
| a | PSE | 115 | 2017 | 2017 | 1500 | 7.03 | 7.03 | 9.00 | 10.14 | 10.12 | 7.55 * | 7.56 | 8.77 | 8.77 |
| b | TX-1 | 13.8 | 240.67 | 240.67 | 3.18 | 17.4 | 17.4 | 0.06 | 10.08 | 10.06 | 0.40 | 0.40 | 8.72 | 8.72 |
| c | C-4 | 13.8 | 237.1 | 237.1 | 3.17 | 14.4 | 14.4 | 0.07 | 9.93 | 9.92 | 0.40 | 0.39 | 8.59 | 8.59 |
| d | C-5 | 13.8 | 229 | 229 | 3.15 | 11.9 | 11.9 | 0.09 | 9.59 | 9.72 | 0.39 | 0.39 | 8.30 | 8.42 |
| e | C-1 | 13.8 | 235.1 | 235.1 | 3.17 | 13.1 | 13.1 | 0.08 | 9.85 | 9.84 | 0.40 | 0.40 | 8.51 | 8.52 |
| f | TX-3 | 2.4 | 77.9 | 77.9 | 0.27 | 14.54 | 14.54 | 0.00 | 18.76 | 18.75 | 0.20 | 0.20 | 16.23 | 16.24 |
| g | TX-4 | 0.48 | 7.27 | 7.27 | 8.82 | 3.8 | 3.8 | 3.68 | 8.75 | 8.75 | 9.30 | 9.30 | 7.57 | 7.57 |
| h | TX-2 | 0.48 | 21.04 | 21.04 | 19.6 | 5.7 | 5.6 | 5.70 | 25.34 | 24.72 | 24.60 | 24.30 | 21.80 | 21.40 |
| M-2 | 2.38 | 2.38 | 0.00 | 17.62 | 17.62 | 0.00 | ||||||||
| M-3 | 5.96 | 5.96 | 0.00 | 25 | 25 | 0.00 | ||||||||
| M-4 | 8.94 | 8.94 | 0.00 | 28.4 | 28.4 | 0.00 | ||||||||
| PNL-1 | 0.48 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | 0.00 | |||||||
| I | C-3 | 0.48 | 17.6 | 17.6 | 5.58 | 3.4 | 3.4 | 1.40 | 21.19 | 20.69 | 12.50 | 12.20 | 18.30 | 17.90 |
| j | C-2 | 0.48 | 17.1 | 17.1 | 5.58 | 3.3 | 3.3 | 1.4 | 20.59 | 20.18 | 12.30 | 12.00 | 17.80 | 17.48 |
| MCC-1 | 0.48 | 2.67 | 2.67 | 0.00 | 14.2 | 14.2 | 0.00 | |||||||
| M-1 | 0.48 | 1.47 | 14.2 | 0.00 | 14.2 | 14.2 | 0.00 | |||||||
| MCC-2 | 0.48 | 1.47 | 1.47 | 0.00 | 4.5 | 4.5 | 0.00 |
* - Based on 1500 SCMVA utility line to ground short circuit MVA. This value is calculated using: MVASLG=SQRT(3)VLLI1ph [ESA Easypower]
Per unit method can be utilized in solving industrial power system short circuits. The figure below shows bus admittance positive and zero sequence per unit matrix for the above system. Negative sequence matrix equals the positive per unit matrix in this example. 2000 MVA and 115kV had been taken as base values.
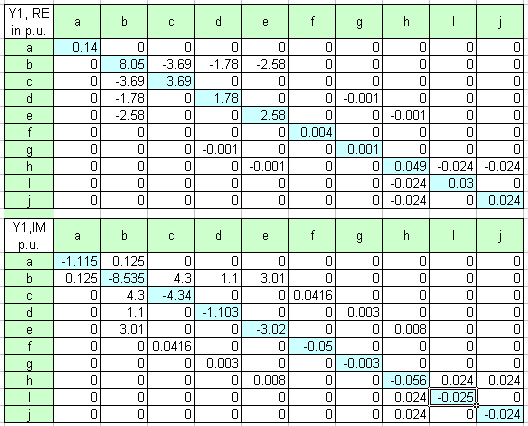
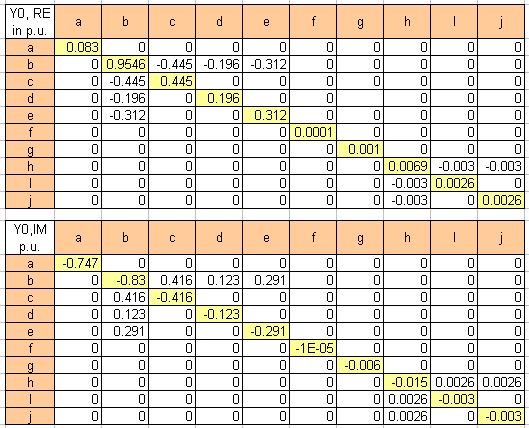
The results of per unit calculations are within 5 percent margin of the MVA method values obtained by running the online calculator. Still, the MVA method does not require a common MVA base as required by the per unit method. Also, per unit method usually ends up with small decimals resulting from converting impedances from one voltage to another or from converting impedances to the same common base. This can easily lead to mistakes in the decimals with resulting wrong or inaccurate answers. Nonetheless, buss admittance sequence network per unit method is indispensable in more advanced short circuit study where voltage drops on other than faulted buss and power flow analysis are being investigated.
Following observation can be made from the performed study:
- Short circuit current values derived from Easypower and the Online Short Circuit Calculator presented on this web-site are by all practical means equal;
- Easypower zero sequence impedance for motors is taken as infinity (no ground return path). Apparently, there is no easy way to accurately calculate short circuits contributed by grounded motors in Easypower. There is no limitation like this when the online short circuit calculator is used for fault analysis.
Copyright © 2019 ARCAD INC. All rights reserved.





