879
Behavior of apparel fabrics during convective and radiant heating
Personal protective equipment (PPE) recommended for arc flash is not always designed for arc flash exposure. The purpose of this paper is to warn of the dangers posed by the use of improper materials in arc flash exposures. The paper also suggests the method of evaluating threshold incident energy for ignition or melting of fabrics as a function of time.
Ignition and melting characteristics of apparel fabrics
The table below shows a representative range of everyday textiles along with some of the measurements of importance in establishing their response towards convective and radiant heating[1]:
| Fabric | Fibre Type | Colour - Finish | Specific mass, kg / m2 | Fabric thickness, mm | Mean ignition (i) or melting (m) temp, C |
|---|---|---|---|---|---|
| Slacks | 65/35 PE/cotton | white - durable pressed | 0.24 | 0.46 | 413i |
| Woven Blouse | 100% PE | yellow | 0.08 | 0.2 | 258m |
| Double Knit | 100% PE | yellow | 0.21 | 0.95 | 250m |
| Denim | 100% cotton | navy blue | 0.3 | 0.58 | 290i |
| Jersey T-Shirt | 100% cotton | white | 0.14 | 0.53 | 305i |
| Slacks | 65/35 PE/cotton | white | 0.24 | 0.48 | 413i |
| Jersey Tube Knit | 100% acrylic | gold | 0.15 | 0.79 | 242m |
| Jersey T-Shirt | 65/35 PE/cotton | white | 0.16 | 0.62 | 435i |
| Terry Cloth | 100% cotton | white | 0.27 | 2 | 302i |
| Batiste | 100% cotton | purple | 0.07 | 0.1 | 438i |
| Tricot | 80/20 acetate/nylon | white | 0.11 | 0.61 | 228m |
| Tricot | 100% nylon | white | 0.09 | 0.27 | 246m |
| Tricot | 100% acetate | white | 0.09 | 0.3 | 230m |
| Taffeta | 100% nylon | white | 0.06 | 0.11 | 241m |
| Slacks | 65/35 PE/cotton | brown | 0.23 | 0.42 | 422i |
| Shirt | 50/50 PE/cotton | white | 0.13 | 0.32 | 355i |
| Batiste | 65/35 PE/cotton | white | 0.09 | 0.19 | 472i |
| Flannel | 100% cotton | white | 0.13 | 0.71 | 305i |
| Flannel FR | 100% cotton | white | 0.15 | 0.69 | 488i |
| Flannel | 100% wool | navy blue | 0.2 | 0.72 | 471i |
Times to ignition or melting of the 20 fabrics in Table above were reported by Wulff[2], [3] for different incident heat fluxes. The Wulff's data have been used to develop a methodology by which ignition and melting times may be forecast. A semi-empirical relationship between ignition/melting time and radiative heat flux has been derived:
where [NF0] is the non-dimensional destruction time of the fabric (that is, time to ignition or melting) and is given by:
where:
(k/l) - average thermal conductance, W / (m2 * C);
t - ignition/melting time, sec;
pl - mass/unit area, kg / m2;
c - average specific heat, W * sec / (kg * C).
NBi is the Biot number which is defined as the ratio of the average convective heat transfer coefficient of the fabric to the average thermal conductance of the fabric. It is obtained experimentally for each fabric.
The non-dimensional radiative heat flux [qxrad] is given by:
where:
ads - adsorptance of the charred fabric;
W0 - incident heat flux, W / m2;
Tim - mean ignition/melting temperature, C;
T0 - ambient temperature, C.
The constants a and b are specific to a particular fabric group and have experimentally derived values.
By substituting the relevant values for a specific fabric and by applying the particular fabric type constants, a and b, an estimate of the ignition or melting time for any incident heat flux can be obtained. Substituting the piloted ignition temperature instead of the self-ignition temperature allows an estimate to be made of the time to piloted ignition. The calculator below computes time to non-piloted ignition or melting of the 20 fabrics as a function of heat flux. It also predicts the amount of incident energy required for self-ignition or melting of the fabrics. The calculator assumes 34C initial textile temperature.
The figure below displays time to damage as a function of radiant heat flux for two different fabrics from the Table 1.
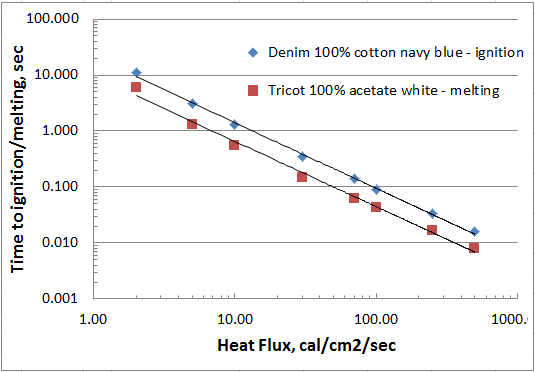
Figure 1. Time to ignition/melting vs radiant heat flux.
The level of intensity and duration of exposure result in a received thermal dose unit TDU that can be calculated and used to estimate these progressive effects from the following equation[4], [1]:
where I is radiated heat flux in W/m2 and t is exposure time in seconds.
Threshold incident energy for ignition or melting of apparel fabrics can be evaluated from Equation 4 above as:
The TDU for melting of nylon and polyester fabrics is ranging from about 1500 to 3000[1] (kW/m2)4/3 * sec. As an example, assuming nylons' TDU is equal to 1500, substituting different time intervals into Equation 5 and converting the calculated onset incident energy for melting of nylon to J/cm2 and cal/cm2:
| Time, sec | Em, J/cm2 | Em, cal/cm2 |
|---|---|---|
| 1 | 16 | 4 |
| 0.1 | 9.4 | 2.3 |
| 0.01 | 5.3 | 1.3 |
How to evaluate threshold incident energy for ignition or melting
Fabric's time to ignition or melting versus heat flux data can be used for determining the textile TDU value. For example, Figure 1 shows that it takes approximately 5cal/cm2/sec heat flux for igniting denim textile listed in Table 1 within 3 seconds time interval. The TDU value for the denim fabric can be calculated by substituting the values for heat flux and time to ignition into Equation 4, and it is roughly equal to 3800(kW/m2)4/3 * sec. Behavior of the fabrics other than those listed in Table 1 during convective and radiant heating can be predicted using a simple test that can be quite easily reproduced in the field.
Incident heat flux can be determined from Equation 4 by exposing the fabric with known TDU unit (the gauge fabric) to a heat source such as a candle lighter at a distance away above the source and taking measurement of time to ignition or melting tim:
The advantage of this approach is that it does not require using calorimeters for measuring incident heat flux. Now, exposing another fabric to heat at the same distance away from the source and taking measurements of time to ignition or melting, TDU can be determined for the test fabric using Equation 4 by substituting incident flux Is and the time to damage for the test fabric. Lastly, the threshold incident energy for ignition or melting of the fabric can be predicted for any exposure time using Equation 5.
Conclusion
While TDU value depends on type of textile, the textile chemical and physical properties, it is seen that the threshold energy for ignition or melting apparel textiles is variable function of heat flux. Any amount of heat delivered within a long enough time interval will have no impact on the fabrics' integrity while a limited amount of heat delivered within short enough time interval may ignite or melt the fabric.
It is also worth noting that the optical response varies widely depending on the fabrics' type, weight and color. For light-colored textiles listed in Table 1, 40 to 60% of IR radiation is reflected, 10 to 40% is transmitted and 14 to 50% is absorbed. The amount of energy exceeding threshold incident energy for a 2nd degree burn for bare skin exposure[5] may pass through protective clothing and destroy the skin before any visible damage is done to the clothing.
NFPA 70E[6] allows flammable clothing with a fabric weight at least 4.5 oz/yd2 ( > 0.16kg/m2) to be worn when working on tasks stated low risk. Stating a task as low risk and allowing the use of apparel fabrics may lead to severe injuries and fatalities from clothing ignitions in arc flash incidents.
The proposed procedure for determining threshold incident energy for ignition or melting might come in handy when verifying that selected personal protective clothing is capable of withstanding the dose it is rated to when the energy is delivered in short duration intense pulse common for arc flash events.
References:
- Ian Hymes, Warren Boydell, 1996, Thermal Radiation: Physiological and Pathological Effects (Belinda Prescott)
- Wulff, W. et al, 1973, Ignition of fabrics under radiative heating, Comb Sci Tech, 6, 321-334
- Wulff, W., 1973, Fabric Ignition, Tex Res J, October, 577-588
- HSE, 2010, Methods of Approximation and Determination of Human Vulnerability for Offshore Major Accident Hazard Assessment
- M. Furtak, L. Silecky, 2012, Evaluation of Onset to Second Degree Burn Energy in Arc Flash, IAEI, July, 65-69
- NFPA 70E, Standard for Electrical Safety in the Workplace
Source
Copyright © 2019 ARCAD INC. All rights reserved.





